Gerakan harmonik sederhana dicipta oleh Ahli Matematik Perancis Baron Jean Baptiste Joseph Fourier pada tahun 1822. Edwin Armstrong (18 DEC 1890 hingga 1 FEB 1954) memerhatikan pergerakan pada tahun 1992 dalam percubaan mereka dan Alexander Meissner (14 SEP 1883 hingga 3 JAN 1958) mencipta pengayun pada bulan Mac 1993. Istilah harmonik adalah perkataan Latin. Artikel ini membincangkan gambaran keseluruhan pengayun harmonik yang merangkumi definisi, jenis dan aplikasinya.

Apa itu Oscillator Harmonik?

Harmonic Oscillator didefinisikan sebagai gerakan di mana daya berkadar terus dengan zarah dari titik keseimbangan dan ia menghasilkan output dalam bentuk gelombang sinusoidal. Daya yang menyebabkan harmonik gerakan dapat dinyatakan secara matematik sebagai

F = -Kx

Di mana,

F = Memulihkan daya

K = Pemalar spring

X = Jarak dari keseimbangan

blok-rajah-of-harmonik-pengayun

Terdapat titik gerakan harmonik di mana sistem berayun, dan daya yang membawa jisim berulang-ulang pada titik yang sama dari mana ia bermula, daya dipanggil kekuatan pemulihan dan titik itu disebut titik keseimbangan atau kedudukan rata-rata. Pengayun ini juga dikenali sebagai pengayun harmonik linear . Tenaga mengalir dari aktif komponen kepada komponen pasif dalam pengayun.

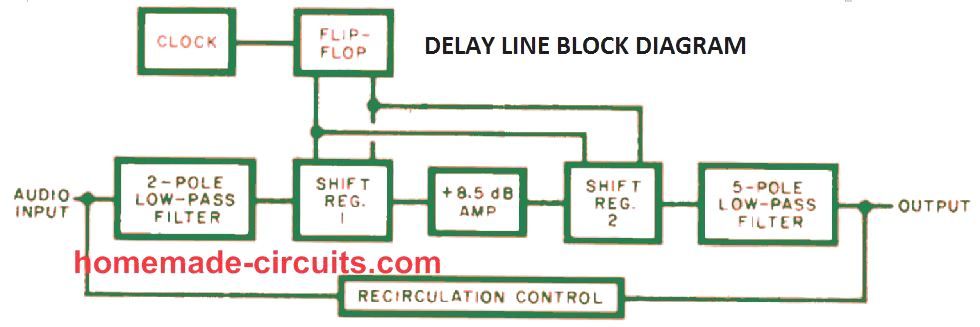
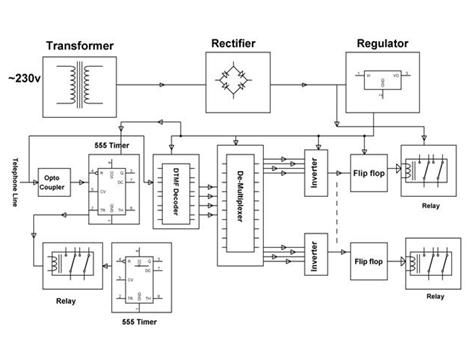
Gambarajah blok

The rajah blok pengayun harmonik terdiri daripada penguat dan rangkaian maklum balas. Penguat digunakan untuk menguatkan isyarat dan isyarat yang diperkuatkan melalui rangkaian maklum balas dan menghasilkan output. Di mana Vi adalah voltan masukan, Vo adalah voltan keluaran dan Vf adalah voltan maklum balas.

Contohnya

Misa pada Musim Bunga: Mata air memberikan daya pemulihan yang mempercepat jisim dan daya pemulihan dinyatakan sebagai

F = ma

Di mana 'm' adalah jisim dan a adalah pecutan.

“jadual kebenaran pintu logik pdf ”

mass-on-a-spring

Spring terdiri daripada jisim (m) dan daya (F). Apabila daya menarik jisim pada titik x = 0 dan hanya bergantung pada kedudukan x - jisim dan pemalar pegas ditunjukkan oleh huruf k.

Jenis Pengayun Harmonik

Jenis pengayun ini merangkumi yang berikut.

Pengayun Harmonik Terpaksa

Apabila kita menerapkan kekuatan luaran pada gerakan sistem, maka gerakan tersebut dikatakan sebagai pengayun harmonik paksa.

Pengayun Harmonik Lembap

Pengayun ini didefinisikan sebagai, ketika kita menerapkan kekuatan luaran ke sistem, maka gerakan pengayun berkurang dan gerakannya dikatakan sebagai gerakan harmonik yang dibasahi. Terdapat tiga jenis pengayun harmonik lembap

redaman-bentuk gelombang

Terlalu Lembap

Apabila sistem bergerak perlahan ke arah titik keseimbangan maka ia dikatakan sebagai pengayun harmonik yang terlalu lembap.

Di Bawah Kelembapan

Apabila sistem bergerak dengan cepat menuju titik keseimbangan maka ia dikatakan sebagai pengayun harmonik yang terlalu lembap.

Kelembapan Kritikal

Apabila sistem bergerak secepat mungkin tanpa berayun mengenai titik keseimbangan maka ia dikatakan sebagai pengayun harmonik yang terlalu lembap.

Kuantum

Ia diciptakan oleh Max Born, Werner Heisenberg, dan Wolfgang Pauli di 'University of Gottingen'. Kata kuantum adalah perkataan Latin dan makna kuantum adalah sejumlah kecil tenaga.

Tenaga Sifar Titik

Tenaga titik sifar juga dikenali sebagai tenaga keadaan tanah. Ia ditentukan apabila tenaga keadaan darat selalu lebih besar daripada sifar dan konsep ini ditemui oleh Max Planck di Jerman dan formula yang dikembangkan pada tahun 1990.

Tenaga Purata Persamaan Osilator Harmonik Sederhana Teredam

Terdapat dua jenis tenaga iaitu tenaga kinetik dan tenaga berpotensi. Jumlah tenaga kinetik dan tenaga berpotensi sama dengan jumlah tenaga.

E = K + U ………………. Persamaan (1)

Di mana E = Jumlah tenaga

K = Tenaga kinetik

U = Tenaga berpotensi

Di mana k = k = 1/2 mv^dua………… persamaan (2)

U = 1/2 kx^dua………… persamaan (3)

nilai-pusingan-bagi-purata- nilai ayunan

Nilai purata tenaga kinetik dan potensi per kitaran ayunan adalah sama dengan

Di mana v^dua= v^dua(KE^dua-x^dua) ……. persamaan (4)

Pengganti eq (4) dalam eq (2) dan eq (3) akan mendapat

k = 1/2 m [b^dua(KE^dua-x^dua)]

= 1/2 m [Aw cos (wt + ø₀)]^dua……. persamaan (5)

U = 1/2 kx^dua

= 1/2 k [Dosa (wt + ø₀)]^dua……. persamaan (6)

Pengganti eq (5) dan eq (6) dalam eq (1) akan mendapat nilai keseluruhan tenaga

E = 1/2 m [b^dua(KE^dua-x^dua)] + 1/2 kx^dua

= 1/2 m w^dua-1/2 m w^duaKE^dua+ 1/2 kx^dua

= 1/2 m w^duaKE^dua+1/2 x^dua(K-mw^dua) ……. persamaan (7)

Di mana mw^dua= K , ganti nilai ini dalam persamaan (7)

E = 1/2 K A^dua- 1/2 Kx^dua+ 1/2 x^dua= 1/2 K A^dua

Jumlah tenaga (E) = 1/2 K A^dua

Tenaga purata untuk satu jangka masa dinyatakan sebagai

KE_purata= U_purata= 1/2 (1/2 K A^dua)

Fungsi Gelombang Pengayun Harmonik

Pengendali Hamiltonian dinyatakan sebagai jumlah tenaga kinetik dan tenaga berpotensi dan dinyatakan sebagai

ђ (Q) = T + V ……………… .eq (1)

Di mana ђ = Operator Hamitonia

T = Tenaga kinetik

V = Tenaga berpotensi

Untuk menghasilkan fungsi gelombang, kita harus mengetahui persamaan Schrodinger dan persamaan dinyatakan sebagai

-đ^dua/ 2μ * d^duaѱ_kami(Q) / dQ^dua+ 1 / 2KQ^duaѱ_kami(Q) = E_kamiѱ_kami(Q) …………. persamaan (2)

Di mana Q = Panjang koordinat normal

Μ = Jisim berkesan

K = Pemalar daya

Syarat had persamaan Schrodinger adalah:

Ѱ (-∞) = ø

Ѱ (+ ∞) = 0

Kita juga boleh menulis eq (2) sebagai

d^duaѱ_kami(Q) / dQ^dua+ 2μ / đ^dua(E_kami-K / 2 * Q^dua) ѱ_kami(Q) = 0 ………… eq (3)

Parameter yang digunakan untuk menyelesaikan persamaan adalah

β = ђ / √μk ……… .. persamaan (4)

d^dua/ dQ^dua= 1 / β^duad^dua/ dx^dua………… .. Persamaan (5)

Pengganti eq (4) dan eq (5) dalam eq (3), maka persamaan pembezaan untuk pengayun ini menjadi

d^duaѱ_kami(Q) / dx^dua+ (2μb^duaE_kami/ đ^dua- x^dua) ѱ_kami(x) = 0 ……… .. persamaan (6)

Ungkapan umum untuk siri kuasa adalah

ΣC¬nx2 …………. persamaan (7)

Fungsi eksponensial dinyatakan sebagai

exp (-x^dua/ 2) ………… persamaan (8)

eq (7) didarabkan dengan eq (8)

ѱυ (x) = ΣC¬nx2exp (-x2 / 2) …………… ..eq (9)

Polinomial hermite diperoleh dengan menggunakan persamaan di bawah

ђ_kami(x) = (-1)^kami* exp (x^dua) d / dx^kami* exp (-x.)^dua) …………… .. persamaan (10)

Pemalar normalisasi dinyatakan sebagai

N_kami= (1/2^kamiυ! √Π)^1/2…………… .eq (11)

The penyelesaian pengayun harmonik sederhana dinyatakan sebagai

Ѱ_kami(x) = N_kamiH_kami(dan) e^{-x2 / 2}……………… persamaan (12)

Di mana N_kamiadalah pemalar Normalisasi

H _kamiadalah orang Hermite

adalah ^{-x2 / dua}adalah orang Gauss

Persamaan (12) adalah fungsi gelombang pengayun harmonik.

Jadual ini menunjukkan istilah pertama polinomial Hermite untuk keadaan tenaga terendah

^kami	0	1	dua	3
H_kami(Y)	1	2y	4y^dua-dua	8y³-12y

Fungsi gelombang dari graf pengayun harmonik sederhana untuk empat keadaan tenaga terendah ditunjukkan dalam rajah di bawah.

gelombang-fungsi-of-harmonic-oscillator

Ketumpatan kebarangkalian pengayun ini untuk empat keadaan tenaga terendah ditunjukkan dalam rajah di bawah.

kebarangkalian -kepadatan -bentuk gelombang

kebarangkalian-ketumpatan-bentuk gelombang

Permohonan

The smenggerakkan pengayun harmonikaplikasi merangkumi yang berikut

Sistem audio dan video
Radio dan alat komunikasi lain
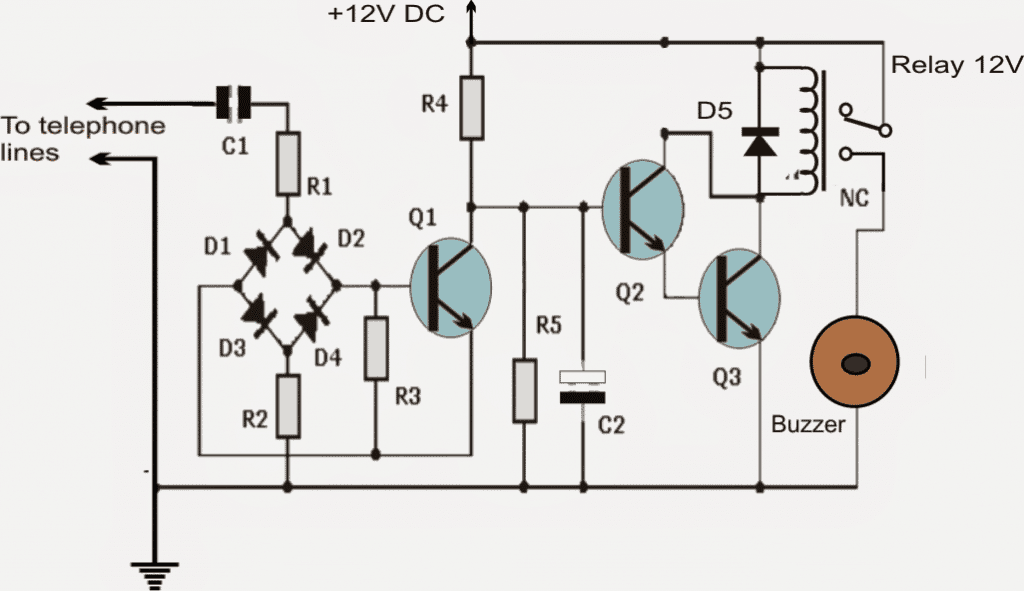
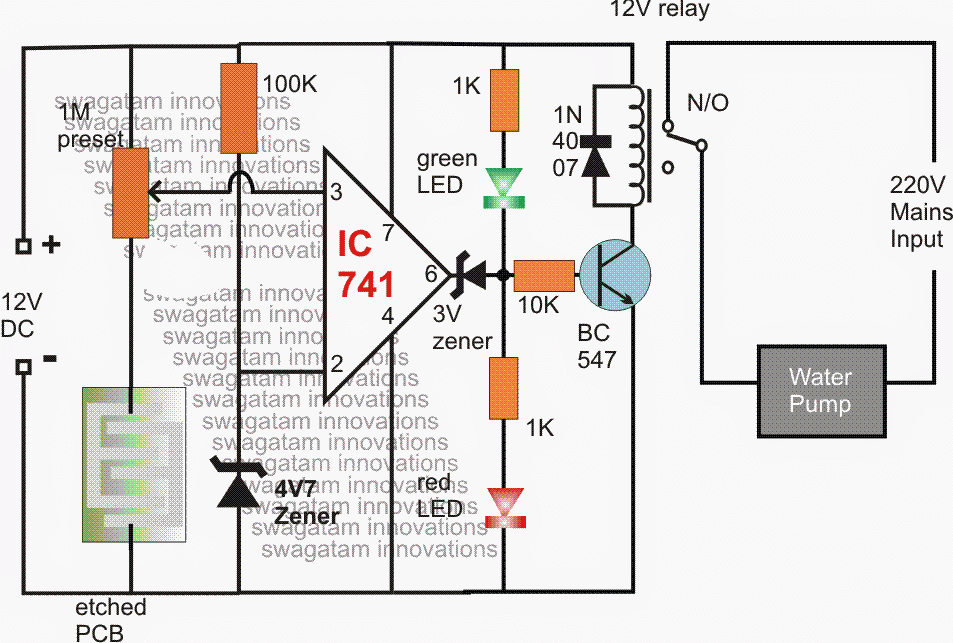
Penyongsang , Penggera
Buzzers
Lampu hiasan

Kelebihan

The kelebihan pengayun harmonik adalah

Murah
Penjanaan frekuensi tinggi
Kecekapan tinggi
Murah
Mudah alih
Ekonomik

Contoh

Contoh pengayun ini merangkumi yang berikut.

Alat muzik
Pendulum sederhana
Sistem spring besar-besaran
Hayun
Gerak tangan jam
Gerakan roda kereta, lori, bas, dll

Ini adalah salah satu jenis gerakan, yang dapat kita perhatikan setiap hari. Harmonik pengayun fungsi gelombang menggunakan Schrodinger dan persamaan osilator harmonik diperoleh. Berikut adalah soalan, apakah jenis gerakan yang dilakukan oleh bungee jumping?